First steps
Getting started with light simulation in GroIMP. Some of this content should be moved to the wiki part and linked here.
–> This content should be moved to “FSP Modelling” as modelling of light is a prerequisite for modelling of photosynthesis.
General Introduction
First steps on light modelling
This tutorial we show you the basics on how to do light modelling in GroIMP. For some more theoretical background pleas refer to the Introduction - A little bit of Theory page. For an advanced tutorial on spectral light modelling check out the Spectral light modelling tutorial.
GroIMP integrates two two main light model implementations, namely:
- Twilight, a CPU-based implementation
- GPUFlux, a GPU-based implementation
While they are both integrating various renderer and light model implementations, they differ in a few details we are not gonna be discuss here. Please refer to the Differences between the CPU and GPU light model page for details. The two main difference however are first that the GPU implementation is several times faster than the CPU implementation and second, that the GPU version is, beside the three channel RGB implementation, able to simulate the full visible light spectrum (spectral light modelling).
In the following, we focus on the three channel RGB versions of both the CPU and GPU implementations.
To set up a light model basically three steps are needed.
- Definition/Initialization of the light model
- Running the light model
- Checking the scene objects for their light absorption
In GroIMP/XL, this can be done as following:
For the Twilight (CPU-based) implementation:
import de.grogra.ray.physics.Spectrum; //constants for the light model: number of rays and maximal recursion depth const int RAYS = 1000000; const int DEPTH = 10; //initialize the scene protected void init() { //create the actual 3D scene [ Axiom ==> Box(0.1,1,1).(setShader(BLACK)) M(2) RL(180) LightNode.(setLight(new SpotLight().(setPower(100),setInnerAngle(0.02),setOuterAngle(0.055)))); ] //make sure the changes on the graph are applied... {derive();} //so that we directly can continue and work on the graph // initialize the light model LightModel CPU_LM = new LightModel(RAYS, DEPTH); CPU_LM.compute(); // run the light model //check the scene objects for their light absorption Spectrum ms; [ x:Box::> { ms = CPU_LM.getAbsorbedPower(x); } ] print("absorbed = "+ms);println(" = "+ms.integrate(), 0xff0000); }
Direct after saving the code, the light model will be executed and the following will be printed in the XL Console Window:
While in the above example the object is black, what means that all incoming radiation is absorbed (and nothing reflected), the line below will shange the object colour to some orange
Axiom ==> Box(0.1,1,1).(setShader(new RGBAShader(1,0.5,0))) M(2) RL(180)
what means that all of red and 50% of green are reflected while all blue radiation is absorbed as the resulting output confirms.
For the GPUFlux (GPU-based) implementation:
import de.grogra.gpuflux.tracer.FluxLightModelTracer.MeasureMode; import de.grogra.gpuflux.scene.experiment.Measurement; //constants for the light model: number of rays and maximal recursion depth const int RAYS = 1000000; const int DEPTH = 10; //initialize the scene protected void init() { //create the actual 3D scene [ Axiom ==> Box(0.1,1,1).(setShader(BLACK)) M(2) RL(180) LightNode.(setLight(new SpotLight().(setPower(100),setInnerAngle(0.02),setOuterAngle(0.055)))); ] //make sure the changes on the graph are applied... {derive();} //so that we directly can continue and work on the graph // initialize the light model FluxLightModel GPU_LM = new FluxLightModel(RAYS, DEPTH); GPU_LM.setMeasureMode(MeasureMode.RGB); // user the Flux model in three channel 'RGB mode' //GPU_LM.setMeasureMode(MeasureMode.FULL_SPECTRUM); //GPU_LM.setSpectralDomain(300,800);// spectral range monitored //GPU_LM.setSpectralBuckets(31);// range divided into 30 buckets GPU_LM.compute(); // run the light model //check the scene objects for their light absorption Measurement ms; [ x:Box::> { ms = GPU_LM.getAbsorbedPowerMeasurement(x); } ] print("absorbed = "+ms);println(" = "+ms.integrate(), 0xff0000); }
For details on spectral light modelling, please refer to Spectral light modelling
Light Sources
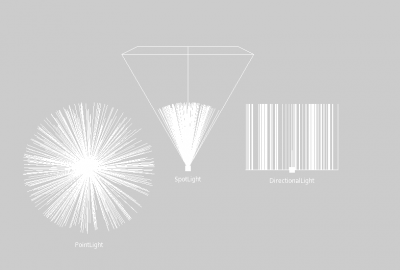
Regarding light sources, GroIMP provides a complete set of possible implementations. They all implement the Light and LightBase interfaces, which makes them easy to handle and exchange. The standard light sources are: PointLight, SpotLight, and DirectionalLight.
The following code places the three light sources next to each other starting with a PointLight on the left, a SpotLight in the middle, and a DirectionalLight on the right.
protected void init () [ Axiom ==> [ Translate(0.0,0,0) LightNode.(setLight(new PointLight())) M(-0.6) TextLabel("PointLight")] [ Translate(0.75,0,0) LightNode.(setLight(new SpotLight())) M(-0.1) TextLabel("SpotLight")] [ Translate(1.5,0,0) LightNode.(setLight(new DirectionalLight())) M(-0.1) TextLabel("DirectionalLight")] ; ]
In the 3D View, they are visualized as a cone for a SpotLight, and as a single line for a DirectionalLight. The PointLight on the left has no visualization.
All light sources provide the functionality of visualizing the light rays emitted by them. To do so, the visualization just need to be activated. Additionally, the number of visualized light rays and their length can be set.
protected void init () [ Axiom ==> LightNode.(setLight(new PointLight().( setVisualize(true), setNumberofrays(400), setRaylength(0.5) ))); ]
The output of the light ray visualization of the three light sources is given below.
Local illumination - Shader
To set the optical properties of an object, in computer graphics the so-called local illumination model is used. It defines so-called shaders, that are define the amount of absorption, reflection and transmission and how the light rays are scattered. The values for absorption are obtained as the 'remaining radiation', i.e., the difference between reflectance and transmission, when we subtract the reflectance and transmission from the total of incoming radiation: Absorption = Total - Reflectance - Transmission.
Note: there is no check of plausibility implemented within the Phong shader. The user needs to make sure that the sum of reflectance and transmission is not higher than the actual incoming radiation. You cannot reflect or transmit more than what was incoming; otherwise, the object would be a light source emitting light.
Computer graphics knows several implementations of local illumination models. The most common are:
- Labertian reflection, and
- Phong shader
Whereas the Lambertian reflection model supports only diffuse reflection, the Phong reflection model (B.T. Phong, 1973) combines ambient, diffuse, and specular light reflections.
Sensors
Sensors or sensor nodes are invisible objects that can be used to monitor light distributions with a scene without interfering with the rest of the scene or the light modelling. For this, GroIMP provides the SensorNode class, a spherical object that can be placed arbitrarily within the scene. To obtain the sensed spectrum, the function getSensedIrradiance() for the Twilight and the getSensedIrradianceMeasurement() function for the GPUFlux light model needs to be called.
Note: The size of the sensor node directly correlates with the probability of got hit by a light ray. For a very small sphere the probability to got hit by a light ray is relatively low, so the number of light rays simulated by the light model needs to be much larger to get repayable results. Therefore, better not to use very small sensor nodes.
Note: The colour of the sensor node determines which wavelengths should be monitored. The default value is white, what stands for 'monitor all colours'. If, for instance, the sensor colour is set to red, only red spectra will be sensed. One can even use smaller values than one, e.g., to sense less parts of a colour - if for whatever reasons this is wanted.
Note: The output of a sensor node is normalized to absorbed radiance per square meter, independent of the actual size of the sensor.
Note: Sensor nodes can be enabled and disabled for the light model using the LM.setEnableSensors(true/false) function. By default they are disabled, since GroIMP version 2.1.4, before they were enabled by default. Having them disabled speeds up the light computation time for scenarios where not sensor nodes are involved.
Below an (incomplete) example for the spectral GPUFlux light model:
import de.grogra.gpuflux.scene.experiment.Measurement; // create a 5cm, white sensor node Axiom ==> SensorNode().(setRadius(0.05), setColor(1, 1, 1)); const FluxLightModel GPU_LM = new FluxLightModel(RAYS, DEPTH); // enable dispersion GPU_LM.setEnableSensors(true); //check what the sensor node has sensed x:SensorNode ::> { Measurement spectrum = GPU_LM.getSensedIrradianceMeasurement(x); float absorbedPower = spectrum.integrate(); ... }
Visualizing light rays
Sometimes it is interesting to see the traces of light rays emitted by a light source when they travel through a scene. In GroIMP, this can be done using the integrated LightModelVisualizer.
To use it, all one needs to do is to add a LightModelVisualizer object into the scene. The two input parameter of the LightModelVisualizer class are defining the number of visualized light rays and the recursion depth the light rays are followed.
To calculate the light rays visualization, the LightModelVisualizer object needs to be selected, ether in the 3D View or 2D Graph Explorer.
protected void init () [ Axiom ==> LightModelVisualizer(175, 10); ]
When selected, go to the Attribute Editor and press 'compute'.
The following scene (given in OpenGL view on the left and Wireframe on the right) contains one spot light with a very slight opening angle, producing a thin beam of light rays that is reflected by several mirrors before finally hitting the end screen or the red sphere in the front.
Please pay attention to the changing colour of the initial white rays when they are reflected or transmitted. Also interesting to notice are the inner reflections within the green box and the red sphere. And keep in mind that only rays that hit an object are visualized.
Given below, is the code to generate the above scene.
/** * To visualize the light rays, select the yellow point at the origin, * go to the 'Attribute Editor' and press 'compute'. */ const Phong MIRROR = new Phong(); const Phong S1 = new Phong(); const Phong S2 = new Phong(); const Phong S3 = new Phong(); static { MIRROR.setSpecular(new Graytone(1));// 1 MIRROR.setDiffuse(new Graytone(0));// 0 MIRROR.setShininess(new Graytone(1));// 1 S1.setDiffuse(new RGBColor(1,0,1)); S1.setDiffuseTransparency(new RGBColor(0,1,0)); S2.setDiffuse(new Graytone(0.4)); S2.setDiffuseTransparency(new Graytone(0.6)); S3.setDiffuse(new RGBColor(1,0,0)); S3.setDiffuseTransparency(new Graytone(0.7)); } module Wall extends Parallelogram(0.6, 0.6); protected void init () [ Axiom ==> LightModelVisualizer(175, 10), ^ RU(90) RL(60) M(0.25) LightNode.(setLight(new SpotLight().(setPower(1000),setInnerAngle(0.0199),setOuterAngle(0.02)))) , ^ Translate(0.7,-1,-0.25) Wall.(setShader(MIRROR)) // mirror 1 , ^ Translate(1.75,1,-0.25) Wall.(setShader(MIRROR)) // mirror 2 , ^ Translate(2.3,0,-0.25) Wall.(setShader(S1)) // semi-transparent , ^ Translate(3.25,1.5,0) Sphere(0.5).(setShader(S3)) , ^ Translate(3.25,-1.25,-0.5) RH(-45) Box(1.5,0.25,2).(setShader(S2)) , ^ Translate(4.5,-2.5,-1.5) RH(45) Parallelogram(3,5).(setShader(BLACK)) ; ]
More light model functions... beyond getAbsorbedPower
So far, we only used the light model to obtain the amount of absorbed power for the objects within our scene, but there is more :)
Note: The following is only implemented for the CPU-based twilight light model of GroIMP and NOT implemented for the GPU-based Flux light model.
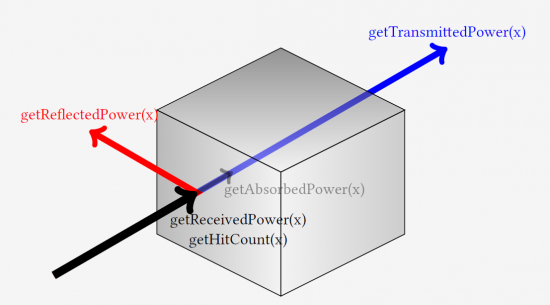
The twilight light model offers further functions, e.g., to obtain the received and transmitted power.
The following code will create a simple scene containing only one flat box on the ground, functioning as test object for now, and a directional light source directly above of it, facing straight downwards.
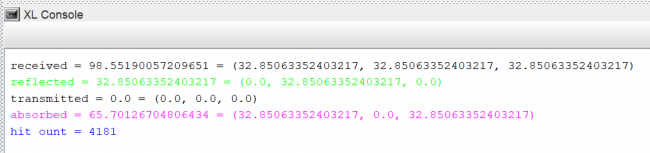
protected void init () [ Axiom ==> // green ground [Null(0,0,0) Box(0.01,1,1).(setShader(GREEN))] //light [ Null(0,0,1) RU(180) LightNode.(setLight(new DirectionalLight().(setPowerDensity(100)))) ]; { clearConsole(); derive(); LightModel LM = new LightModel(10000, 5); LM.compute(); } x:Box ::> { println("received = "+LM.getReceivedPower(x).integrate() +" = "+ LM.getReceivedPower(x),0x000000); println("reflected = "+LM.getReflectedPower(x).integrate() +" = "+ LM.getReflectedPower(x),0x00ff00); println("transmitted = "+LM.getTransmittedPower(x).integrate() +" = "+ LM.getTransmittedPower(x),0x000000); println("absorbed = "+LM.getAbsorbedPower(x).integrate() +" = "+ LM.getAbsorbedPower(x),0xff00ff); println("hit count = "+LM.getHitCount(x),0x0000ff); } ]
When the code is saved, it generates the scene and directly calls the light model and obtains the set of properties of the box object, including
- getReceivedPower, returns the received power
- getReflectedPower, returns the reflected power
- getTransmittedPower, returns the transmitted power
- getAbsorbedPower, returns the absorbed power
- getHitCount, returns the number of light rays that have hit the object
The output of the code is given below:
As expected for a green object and a pure white light source, we see that green is totally reflected while red and blue are totally absorbed. Since we have not defined any transparency for the box, the transmitted part is empty.
As usual, the properties can be obtained for the three colour channels induvially or integrated using the integrate() function.
Note: For white light, the obtained values should reflect the settings of the used shader - for objects that have received most direct light. When the scene is getting more complex and several reflections involved, and therefore the input light is not white anymore, the results will become a combination of the whole incoming radiation.
Sensor Grids and Areal Sensors
Light distributions, micro-light climate, light above canopy, light extinction coefficients, etc. are key parameters for any canopy simulations. To obtain these, areal or gird like sensor arrangements are required. Both can be generated within GroIMP by only a few lines of code.
For an introduction to SensorNnodes have a look at the Sensors tutorial.
Spectral Light Modelling
These three core aspects of light simulation—global and local illumination models, and light sources—are the base for any light simulation. When it comes to spectral light simulations, specialized implementations of the aforementioned aspects are required, capable of simulating not only one or three light channels, as is typical for common light models, but also the entire light spectrum for different wavelengths.
Note: The hardware requirement for performing GPU-based ray tracing is a programmable graphics card with OpenCL support. For example, any Nvidia card will do well, whereas older versions of integrated Intel cards—as they are often used in laptops—are not suitable for this. GPUFlux supports multiple GPU units and CPUs working in parallel at the same time. The use of multiple devices as well as the use of the CPU needs to be activated within the Preferences of the Flux renderer; see image below.
Spectral light simulations now deal not only with the pure calculation of light distributions it's intensity (or quantity), and duration, but further includes the aspect of light quality.
The main factor influencing light quality is the light's spectral composition (of which the part visible to the human eye is often simply referred referred to as colour). Thus, the compositions of different intensities of different wavelengths form the final light spectrum or colour. Below are the light spectra of typical sunlight, of common HPS lamps (high-pressure sodium lamps), as used for instance as additional light sources within greenhouses, and a red LED lamp.
Effect of spectral light on morphogenesis
Open SpectralLight.gsz and explore the four files it consists of: Main.rgg, Modules.rgg, Parameters.rgg, and KL.java. The names already suggest that in Main.rgg you will find the main parts of the model, notably the methods init() and grow(), but also methods to create and update the graphical output on charts (initChart() and updateChart()); in Modules.rgg the definition of all modules used in the model; in Parameters.rgg all parameters; and finally we have again the photosynthesis model KL.java.
What can this model do? Well, as its name suggests, with this model we can simulate spectral light. So, instead of just simulating a lamp with white light or, at best, red, green and blue light, we now have the possibility to simulate an entire spectrum of visible light and even part of the light just outside the visible spectrum!
Open Parameters.rgg and inspect the lines 8 to 22:
//redLED.spd, blueLED.spd static const float[] WAVELENGTHS = {360, 361, 362, 363, 364, 365, 366, 367, 368, 369, 370, 371, 372, ...}; static const float[] WAVELENGTHS_PB = {380, 381, 382, 383, 384, 385, 386, 387, 388, 389, 390, 391, ...}; //red static const float[] AMPLITUDES_RED = {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...}; //blue static const float[] AMPLITUDES_BLUE = {0.011596, 0.011512, 0.00871, 0.002914, 0, 0, 0.002729, 0.007988, ...}; //far-red static const float[] AMPLITUDES_FR ={0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...}; //lamp phenobean static const float[] AMPLITUDES_PHENOB = {7.26375E-05, 0.00023939, 0.000212121, 0.000233373, 0.00020509, 0.000166495, 0.000155523, 0.000184755, 0.000256009, 0.000169664, 0.000140593, 0.000194424, 0.000196017, 0.000221532, 0.000192043, 0.000193233, ...};
Here you will find long arrays of numbers, first of all two arrays with wavelengths between 360(380) and 830 (780) nm, at a resolution of 1 nm. In the second array, “PB” stands for “Phenobean”, and it designates the lamps installed in the PHENOBEAN phenotyping chamber (one of our facilities at Institut Agro in Angers, France).
The following four arrays (L. 12 – 22) yield the amplitude data for red, blue, far red and phenobean LED lamps, whereas the constants in L. 25 – 27 give correction factors to arrive at a PAR output of 52 µmol/m2 per light string, the nominal output power.
To see the process of construction of the different lamp types we have to go to Modules.rgg: In lines 8 to 65 we see the definitions of six lamp modules, of which two blue, two red, one Phenobean, and one far-red. Two red and two blue, because we want top- and interlighting. A lamp is constructed by creating an irregular spectral curve, containing the spectral distribution of light, combined with a PhysicalLight object using the physical distribution (defined in L. 109ff of Parameters.rgg: this is a double array containing the spatial information: azimuth and elevation of the light beam, from its origin).
We have visualized the beams so that you can see them in the scene: at the moment there are five lamps in the scene, they are defined in L. 25 – 29 of Main.rgg in the init() method:
==>> ^ M(70) RU(180) RedLEDtop; ==>> ^ M(70) RU(180) Translate(0,20,0) BlueLEDtop; ==>> ^ M(40) RU(180) RL(45) Translate(0,0,-50) RedLED; ==>> ^ M(40) RU(180) FRLED;//RedLEDtop;//FRLED; / ==>> ^ M(50) RU(180) Translate(0,30,0) FRLED;//RedLEDtop;//FRLED;//PHENOBLED;
You can see in the commented block that we have already used several lamps. You can do the same: change the composition of lamps as you like, save the code file, and then on Render View → Flux renderer, to see the color combination.
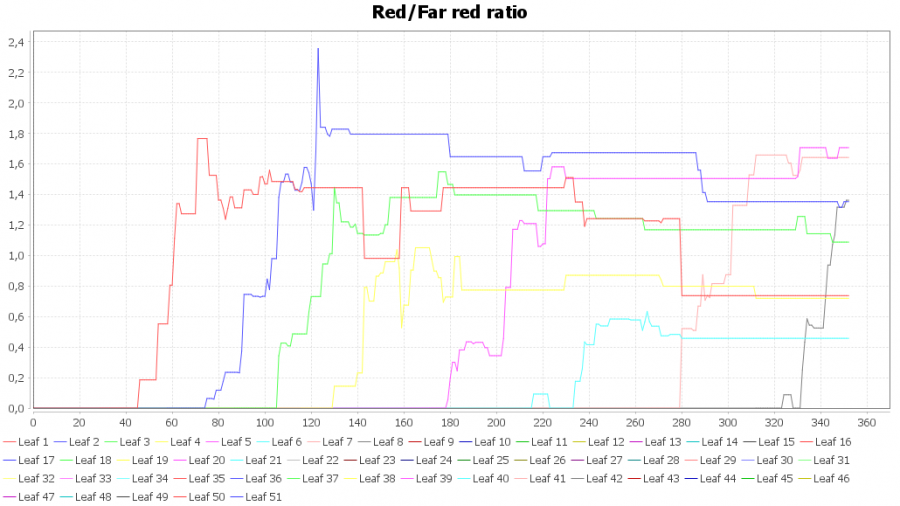
You may then click on the Run grow button to see some output: First of all, you note that there are several charts: Leaf surface dynamics (to monitor the leaf surface of each leaf rank), then Internode length dynamics (for each internode rank), Red/Far red ratio, Phytochrome ratio, and Absorbed spectrum. Starting with the last item, Absorbed spectrum actually gives out the light absorbed per leaf rank, but for each “bucket” of about 2.6 nm wavelength, so you can see how much blue, green, red and far red light each leaf is actually absorbing (we can only guess how much of this is transmitted and reflected but all of this must add up to 100%…). How does this work? Have a look at the definition of the Leaf (Modules.rgg, L. 82ff):
module Leaf (int ID, super.length, super.width, float al, int age, int rank, Measurement ms, float rfr, float absred, float absfarred, float absblue, float as) extends Box(length, width, 0.01){ { Phong myShader = new Phong(); myShader.setDiffuse(reflectionSPD); myShader.setDiffuseTransparency(transmissionSPD); //ColorGradient colorMap = new ColorGradient("one",0,250, graphState(), 0); setShader(new AlgorithmSwitchShader(new RGBAShader(0,1,0), myShader, leafmat));} float getSurface() { float SCF = 1000; return this.length*this.width*SCF; } };
We note that Leaf has a lot of parameters apart from its length and width, the absorbed light al and the amount of assimilates as: We will come back to that later. Let’s first of all explore the shader of the leaf, it’s called a Phong shader, named after the researcher who worked on this topic. Using such a Phong shader allows you to specify spectra for reflection and transmission (methods setDiffuse() and setDiffuseTransparency()). The arguments for these methods are two arrays with numbers containing the amount of light reflected and transmitted per waveband, based on measurements using a spectrophotometer). The two arrays can be found at the very end of Parameter.rgg (they are in fact curves that are constructed with the static statement in L. 397-401 using data from other arrays (L. 257ff).
Back to the definition of the Leaf module: you note that one of its parameters is called ms and it’s of a type we’ve never seen before: Measurement. Let’s see how this is used: go to Main.rgg, L. 63. Here we see in the method absorbAndGrow() that the parameter ms of Leaf is updated:
lf[ms] = lm.getAbsorbedPowerMeasurement(lf);
A measurement is in fact a data table, in which the absorbed spectrum is stored, one measurement per wavelength. This is done by an extended light model called FluxLightModel. A spectral measurement can now be used in several ways: we can output the data to a graph and display the absorbed spectrum as is done in L. 140 of Main.rgg. Or we can pick specific wavelengths such as the peaks of absorbed blue (450 nm), red (630 nm), and far red (760 nm) and store them in the previously defined variables absblue, absred and absfarred (L. 132 – 134).
lf[absblue] = lf[ms].data[19]; //450 nm lf[absred] = lf[ms].data[86]; //630 nm lf[absfarred] = 0.0001 + lf[ms].data[135]; // 760 nm
It is then quite easy to calculate the red/far red ratio (L. 135), which is another one of the variables of Leaf.
lf[rfr] = lf[absred]/lf[absfarred];
The R/FR ratio is translated within the plant into an equilibrium ratio of two forms of phytochromes Pr and Pfr. This is not a linear relation; therefore we need to employ another function that we called calcPhytochrome(), defined in L. 75-82 of Parameters.rgg:
public static double calcPhytochrome(float rfr) { double phi = 0; double Zpfr = 1.7; // slope parameter double phiR = 0.75; // value of phi at high R:FR double phiFR = 0.03; // value of phi at R:FR = zero; return phi = 1 - (rfr + Zpfr) / ( (rfr/(1-phiR)) + (Zpfr/(1-phiFR)) ); }
The function basically defines the response curve of phytochrome ratio to R/FR. You can see the dynamic output in the graphs “Red/Far red ratio” and “Phytochrome ratio”.
What is the effect of different wavelengths on plant morphology? There are several, but it is known that a low R/FR will enhance internode length and leaf surface, and that blue light will have the opposite effect. Also, blue light will have a delaying effect on the phyllochrone. We have added a number of functions to this effect, that will modify the parameters of the logistic growth function for internodes and leaves, as a function of R/Fr and absorbed blue light (methods “maxlength”, “intslope”, and “phyllochron”, L. 83-106 in Parameters.rgg).
public static double maxlength(float absblue, float rfr) { float residual = 0.15; float phi = calcPhytochrome(rfr); float ml = residual + (Math.exp(-phi-25*absblue)); return ml; } public static double intslope(float absblue, float rfr) { float residual = 0.01; float phi = calcPhytochrome(rfr); float isl = residual + 0.1*Math.exp(-phi-25*absblue); //println("intslope: " + isl); return isl; } public static int phyllochron(int rank, int id) { if(rank>3) {Leaf lef = first((* lf:Leaf, (lf[rank]==rank-1 && lf[ID]==id)*)); float phi = calcPhytochrome(lef[rfr]); return (int) (28 + 8*Math.exp(-10*lef[absblue]+2*phi));} else { return 28;} }
Tasks: 1) Run the model with different lamp configurations! Observe the effect on internode length and leaf surface dynamics!
2) Run the model for a number of steps, then move a lamp*, or change its power output! You can also add a Sky light source but beware that this has a dramatic effect on the R/FR ratio (hint! To prevent this, you have to increase the power output of the two far red lamps as it currently is too low). Once you have added a Sky light, you can also have a look at the Photosynthesis rate dynamics (for some reason, the light output of the LED lamps alone is a bit too low).
3) Open the Excel file Spectre.xlsx and inspect the way the relation between absorbed blue and rfr and slope/maximum dimension has been implemented!
4) Currently we have only one plant in the scene: go to Parameters.rgg, L. 45, 46 and 49 and modify the parameters so that you get 25 plants (5 x 5), with plant number 13 being the chosen one! Then run the model again to see if the plants will develop differently!
*To move a lamp, you can click on its tip and then drag the lamp into one direction (x, y z) by clicking, holding and moving one of the three arrowheads. If selection in the scene doesn’t work you can try finding the lamp using the Flat Object Inspector window that is already open in your model:
Differences between the CPU and GPU light model
1. Ordered List Item
2. Interpretation of specular and shininess reflection
3. Interpretation of transparency of image textures
4. Implementation of the GrinClonerNode behaviour
- CPU (Twilight) implementation: repeats objects only into first quadrant
- GPU (Flux) implementation: repeats objects into all four quadrants
5. Only in the Twilight light light model the additional function of getReceivedPower, getReflectedPower, getTransmittedPower, getAbsorbedPower, and getHitCount are implemented. See: More light model functions... beyond getAbsorbedPower
In this tutorial we will see how to get started with a FluxModel in GroIMP.
Go here to see more about how the FluxModel is defined in GroIMP.
Light Model
First, we setup of the Flux Light Model:
import de.grogra.gpuflux.tracer.FluxLightModelTracer.MeasureMode; import de.grogra.gpuflux.scene.experiment.Measurement; const int RAYS = 10000000; const int DEPTH = 10; const FluxLightModel LM = new FluxLightModel(RAYS, DEPTH); protected void init () { LM.setMeasureMode(MeasureMode.FULL_SPECTRUM); LM.setSpectralBuckets(81); LM.setSpectralDomain(380, 780); }
This is:
- importing of the needed classes
- initializing the model with 10 million rays and a recursion depth of 10
- setting the parameters with 400nm divided into 80 buckets of 5nm.
Then, run the light model and determine the amount of sensed radiation or of absorbed power for an object-type.
public void run () [ { LM.compute(); } x:SensorNode ::> { Measurement spectrum = LM.getSensedIrradianceMeasurement(x); float absorbedPower = spectrum.integrate(); //... } x:Box ::> { Measurement spectrum = LM.getAbsorbedPowerMeasurement(x); float absorbedPower = spectrum.integrate(); //... } ]
This is:
- computing the model
- computing the integration of the whole absorbed spectrum for both
- sensor nodes
- box objects
Demonstration of the method for the determination of the amount of absorbed power per bucket or integration over a certain spectral range.
Measurement spectrum = LM.getAbsorbedPowerMeasurement(x); //absorbed power for the first bucket: 380-385 nm float ap380_385 = spectrum.data[0]; //accumulate absorbed power for the first four 50 nm buckets float b0 = 0, b1 = 0, b2 = 0, b3 = 0; for (int i:(0:10)) { b0 += spectrum.data[i]; b1 += spectrum.data[i + 10]; b2 += spectrum.data[i + 20]; b3 += spectrum.data[i + 30]; } //integrate the whole spectrum float ap = spectrum.integrate();
This is:
- Getting the absorbed spectrum
- Storing the first bucket in a variable
- building four integrals, each of 50 nm (10 buckets of 5 nm) and sum up the first 40 buckets.
- calculating the integral over the whole spectrum.